9-Bus System (System I)

I. Introduction:

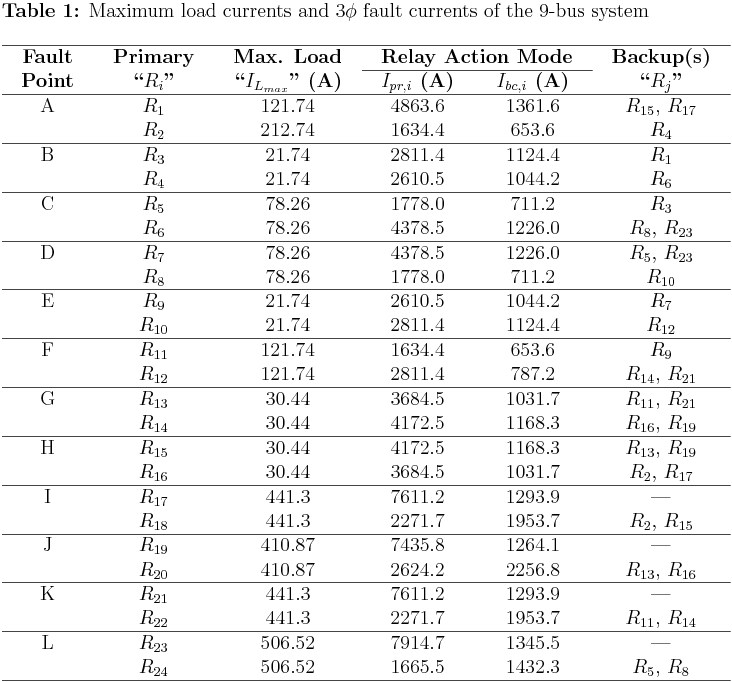
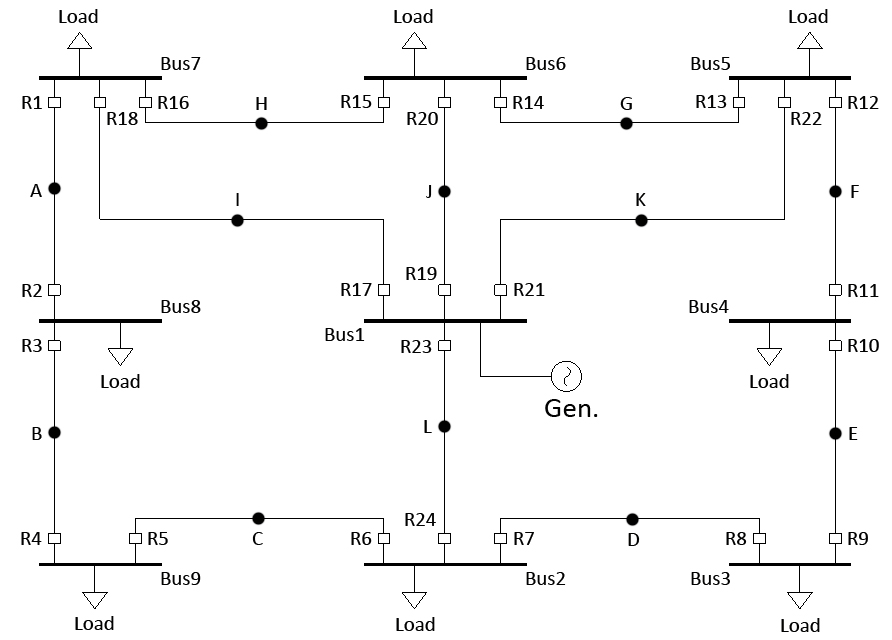
\(\bullet\) In this test system, 9-bus interconnected distribution system with one single-end fed and equal impedances for all the lines is considered.
\(\bullet\) This system assumes a \(3\phi\) fault at the midpoint of each line, as shown in the figure given below, with no backup protection for relays \(\{R_{17},R_{19},R_{21},R_{23}\}\).
\(\bullet\) Bus 1 is supplied by a power source of  \(100 \text{ MVA}\), \(33 \text{ kV}\) with a source impedance of \((0+j0.1) \ \text{p.u}\). Also, all the lines have an impedance of \((0+j0.2) \ \text{p.u}\).
\(\bullet\) The CT ratio (\(CTR\)) of all the directional overcurrent relays (DOCRs) is \(500:1\), and all these DOCRs are considered to be numerical, in which both plug-setting (\(PS\)) and time-multiplier setting (\(TMS\)) are continuous.
\(\bullet\) The lower and upper bounds of \(PS\) of each DOCR are calculated based on the following practical equaltions:
$$PS^{min}_{i} = \frac{OLF \times I_{n,i}}{CTR} \text{..... (1)}$$
$$PS^{max}_{i} = \frac{2}{3 CTR} I^{min}_{f,i} \text{..... (2)}$$
where \(I_{n,i}\) is the nominal current rating of the circuit protected by the relay \(R_i\). \(OLF\) is the overload factor (with \(OLF=1.25\)), and \(I^{min}_{f,i}\) is the minimum fault current that should be detected by the \(i\)th relay.
\(\bullet\) In addition, relays \(\{R_{17},R_{19},R_{21},R_{23}\}\) are assumed with no backup.
\(\bullet\) Also, the minimum operating time of each relay \(T^{min}\) is taken as 0.2 s.
\(\bullet\) The rest data is given below (click on them for bigger size):

II. Single-Line Diagram:

\(\bullet\) This single-line diagram was drawn by Ali R. Al-Roomi in Sept. 2013 and all the necessary data were coded in MATLAB m-files.

III. Files:

\(\bullet\) System DATA (MATLAB, m-file Format) [Download]
\(\bullet\) Results Tester (MATLAB, m-file Format) [Download]

IV. Citation Policy:

If you publish material based on databases obtained from this repository, then, in your acknowledgments, please note the assistance you received by using this repository. This will help others to obtain the same data sets and replicate your experiments. We suggest the following pseudo-APA reference format for referring to this repository:

Ali R. Al-Roomi (2015). Optimal Relay Coordination Test Systems Repository [https://www.al-roomi.org/coordination]. Halifax, Nova Scotia, Canada: Dalhousie University, Electrical and Computer Engineering.

Here is a BiBTeX citation as well:

@MISC{Al-Roomi2015,
author = {Ali R. Al-Roomi},
title = {{Optimal Relay Coordination Test Systems Repository}},
year = {2015},
address = {Halifax, Nova Scotia, Canada},
institution = {Dalhousie University, Electrical and Computer Engineering},
url = {https://www.al-roomi.org/coordination}
}

V. References:

[1] Ali R. Al-Roomi. Optimal Coordination of Power Protective Devices with Illustrative Examples. Hoboken, New Jersey: Wiley-IEEE Press, 2022.
[2] F. A. Albasri, A. R. Alroomi, and J. H. Talaq, "Optimal Coordination of Directional Overcurrent Relays Using Biogeography-Based Optimization Algorithms," IEEE Transactions on Power Delivery, vol. 30, no. 4, pp. 903–911, 2015.