I. Introduction:

\(\bullet\) This system contains thirteen generating units with a load demand of 1800 MW. Some researchers could evaluate their proposed optimization algorithms with different load demands.
\(\bullet\) The fuel-cost function of this test system is modeled using the quadratic cost function as follows:

\(C_i\left(P_i\right) = a_i + b_i P_i + c_i P^2_i \) .......... \((1)\)

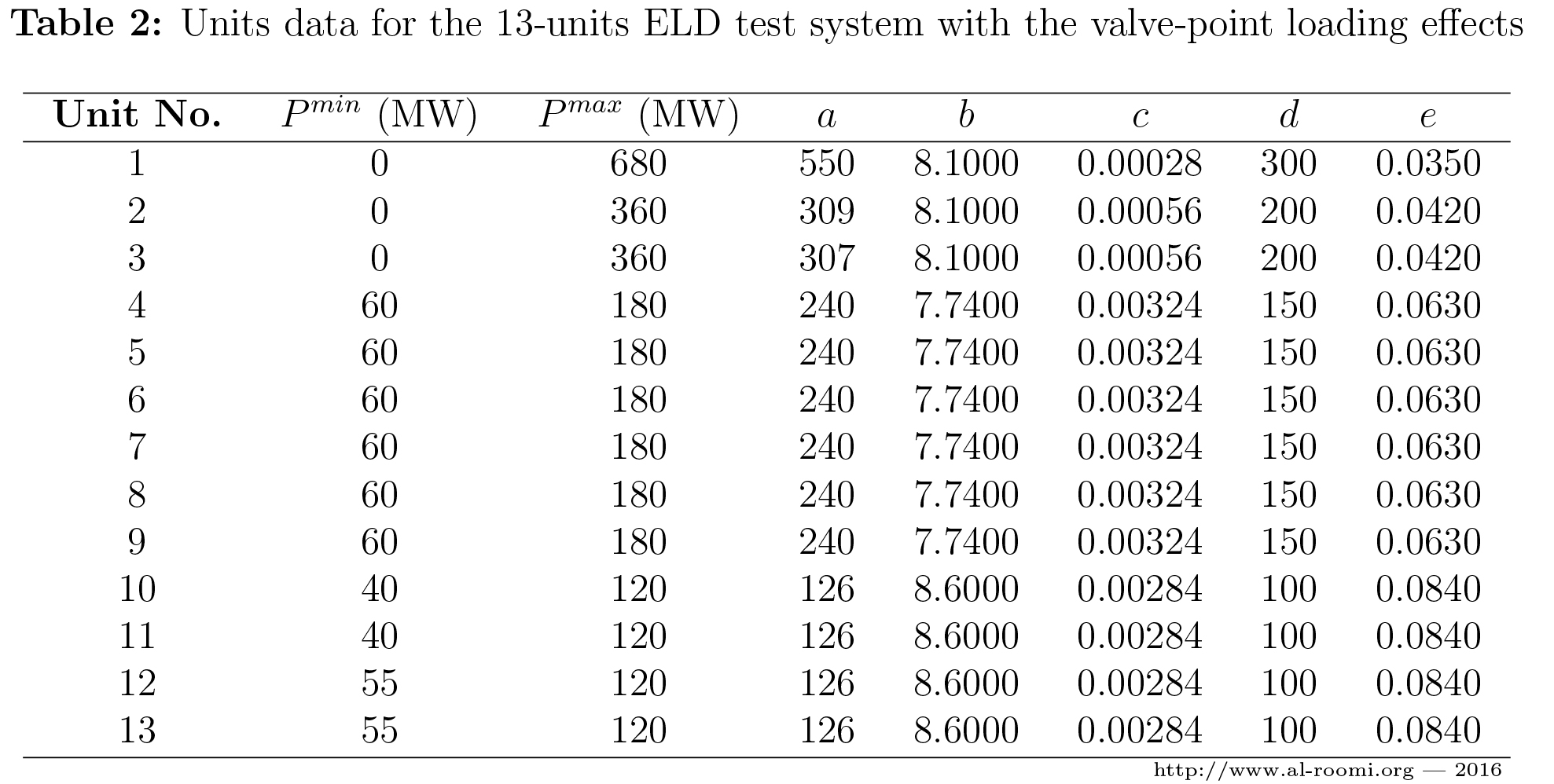
   where \(a_i\), \(b_i\), and \(c_i\) are the function coefficients and tabulated in Table 1.

\(\bullet\) If the valve-point loading effects are considered, then (1) becomes:

\(C_i\left(P_i\right) = a_i + b_i P_i + c_i P^2_i + \left|d_i \times \sin\left[e_i \times \left(P_i^{min} - P_i\right) \right]\right|\) .......... \((2)\)

   where \(d_i\) and \(e_i\) are the coefficients of the valve-point loading effects. Thus, Table 1 is expanded to Table 2.

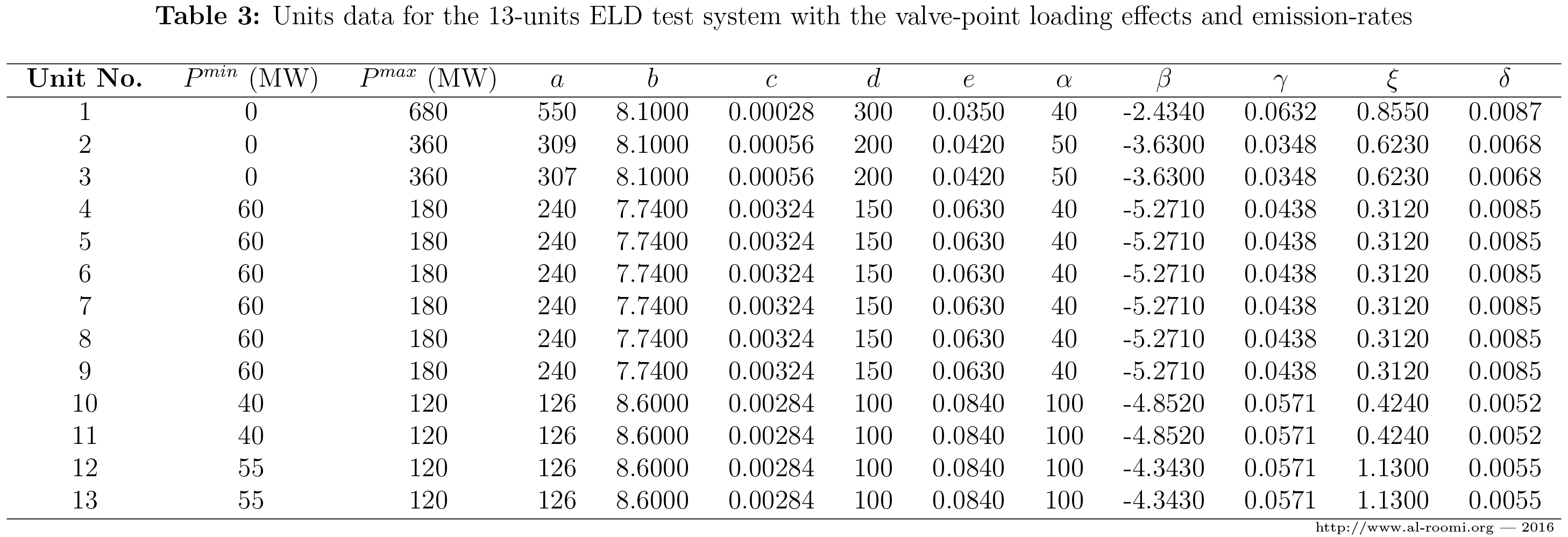
\(\bullet\)  If the emission-rates are considered, then the following equation can be used to express these rates in the optimization problem:

\(E\left(\sum_{i=1}^n P_i\right) = \sum_{i=1}^n 10^{-2} \left(\alpha_i + \beta_i P_i + \gamma_i P^2_i \right) + \xi_i e^{\delta_i P_i}\) .......... \((3)\)

   where \(\alpha_i\), \(\beta_i\), \(\gamma_i\), \(\xi_i\), and \(\delta_i\) are the coefficients of the \(i\)th unit emission characteristics. Thus, Table 2 is expanded to Table 3 [13].

II. Files:

\(\bullet\) System Data (Text Format) [Download]

III. Citation Policy:

If you publish material based on databases obtained from this repository, then, in your acknowledgments, please note the assistance you received by using this repository. This will help others to obtain the same data sets and replicate your experiments. We suggest the following pseudo-APA reference format for referring to this repository:

Ali R. Al-Roomi (2016). Economic Load Dispatch Test Systems Repository [https://www.al-roomi.org/economic-dispatch]. Halifax, Nova Scotia, Canada: Dalhousie University, Electrical and Computer Engineering.

Here is a BiBTeX citation as well:

@MISC{Al-Roomi2016,
author = {Ali R. Al-Roomi},
title = {{Economic Load Dispatch Test Systems Repository}},
year = {2016},
address = {Halifax, Nova Scotia, Canada},
institution = {Dalhousie University, Electrical and Computer Engineering},
url = {https://www.al-roomi.org/economic-dispatch}
}

IV. References (Some selected papers that use this test system):

[1] N. Sinha, R. Chakrabarti, and P. K. Chattopadhyay, “Evolutionary Programming Techniques for Economic Load Dispatch,” IEEE Trans. Evol. Comput., vol. 7, no. 1, pp. 83–94, Feb. 2003.
[2] T. A. A. Victoire and A. E. Jeyakumar, “Hybrid PSO-SQP for Economic Dispatch with Valve-Point Effect,” Electr. Power Syst. Res., vol. 71, no. 1, pp. 51–59, 2004.
[3] C.-L. Chiang, “Improved Genetic Algorithm for Power Economic Dispatch of Units With Valve-Point Effects and Multiple Fuels,” Power Syst. IEEE Trans., vol. 20, no. 4, pp. 1690–1699, Nov. 2005.
[4] C. H. Chen and S. N. Yeh, “Particle Swarm Optimization for Economic Power Dispatch with Valve-Point Effects,” in Transmission Distribution Conference and Exposition: Latin America, 2006. TDC ’06. IEEE/PES, 2006, pp. 1–5.
[5] L. dos Santos Coelho and V. C. Mariani, “Combining of Chaotic Differential Evolution and Quadratic Programming for Economic Dispatch Optimization with Valve-Point Effect,” IEEE Trans. Power Syst., vol. 21, no. 2, pp. 989–996, May 2006.
[6] C. C. Kuo, “A Novel Coding Scheme for Practical Economic Dispatch by Modified Particle Swarm Approach,” IEEE Trans. Power Syst., vol. 23, no. 4, pp. 1825–1835, Nov. 2008.
[7] L. dos S. Coelho and V. C. Mariani, “An Improved Harmony Search Algorithm for Power Economic Load Dispatch,” Energy Convers. Manag., vol. 50, no. 10, pp. 2522–2526, Jul. 2009.
[8] T. Niknam, “A New Fuzzy Adaptive Hybrid Particle Swarm Optimization Algorithm for Non-Linear, Non-Smooth and Non-Convex Economic Dispatch Problem,” Appl. Energy, vol. 87, no. 1, pp. 327–339, Jun. 2010.
[9] S. Duman, U. Güvenç, and N. Yörükeren, “Gravitational Search Algorithm for Economic Dispatch with Valve-Point Effects,” Int. Rev. Electr. Eng., vol. 5, no. 6, pp. 2890–2895, 2010.
[10] J. S. Alsumait, J. K. Sykulski, and A. K. Al-Othman, “A Hybrid GA-PS-SQP Method to Solve Power System Valve-Point Economic Dispatch Problems,” Appl. Energy, vol. 87, no. 5, pp. 1773–1781, Nov. 2010.
[11] S. Hemamalini and S. P. Simona, “Artificial Bee Colony Algorithm for Economic Load Dispatch Problem with Non-smooth Cost Functions,” Electr. Power Components Syst., vol. 38, no. 7, pp. 786–803, May 2010.
[12] T. Niknam, H. D. Mojarrad, and H. Z. Meymand, “A Novel Hybrid Particle Swarm Optimization for Economic Dispatch with Valve-Point Loading Effects,” Energy Convers. Manag., vol. 52, no. 4, pp. 1800–1809, Jan. 2011.
[13] S. Rajasomashekar and P. Aravindhababu, “Biogeography Based Optimization Technique for Best Compromise Solution of Economic Emission Dispatch,” Swarm Evol. Comput., vol. 7, pp. 47–57, Jun. 2012.
[14] G. Xiong, D. Shi, and X. Duan, “Multi-Strategy Ensemble Biogeography-Based Optimization for Economic Dispatch Problems,” Appl. Energy, vol. 111, pp. 801–811, Jun. 2013.
[15] K. Zare and T. G. Bolandi, “Modified Iteration Particle Swarm Optimization Procedure for Economic Dispatch Solving with Non-Smooth and Non-Convex Fuel Cost Function,” in 3rd IET International Conference on Clean Energy and Technology (CEAT) 2014, 2014, pp. 1–6.
[16] R. Arul, G. Ravi, and S. Velusami, “An Improved Harmony Search Algorithm to Solve Economic Load Dispatch Problems with Generator Constraints,” Electr. Eng., vol. 96, no. 1, pp. 55–63, 2014.
[17] T. H. Khoa, P. M. Vasant, M. S. B. Singh, and V. N. Dieu, “Solving Economic Dispatch Problem with Valve-Point Effects Using Swarm-Based Mean-Variance Mapping Optimization (MVMO),” Cogent Eng., vol. 2, no. 1, pp. 1–18, Aug. 2015.