IEEE 15-Units ELD Test System

I. Introduction:

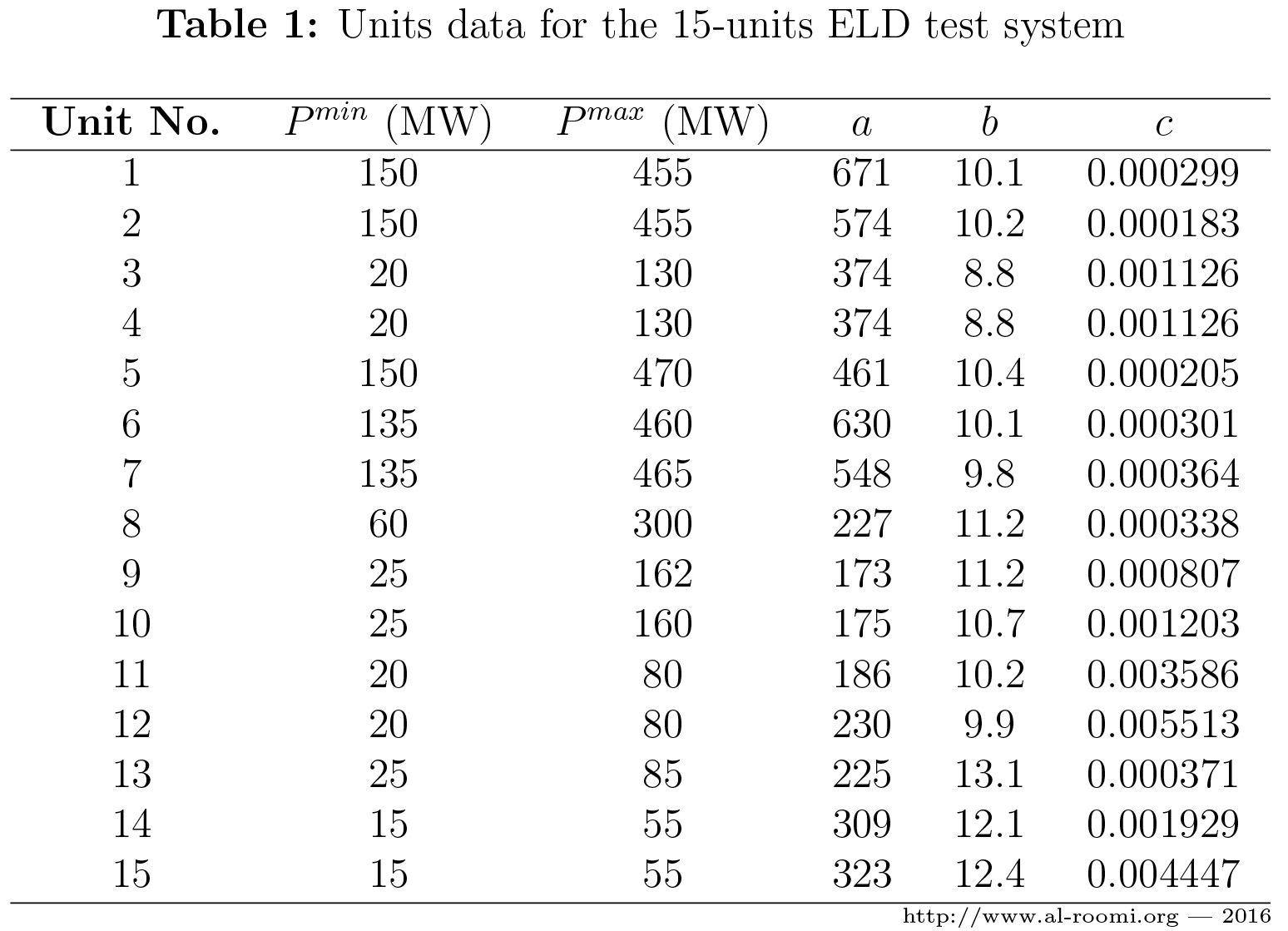
$\bullet$ This system contains fifteen generating units with a load demand of 2630 MW. Some researchers could evaluate their proposed optimization algorithms with different load demands.
$\bullet$ The fuel-cost function of this test system is modeled using the quadratic cost function as follows:

$C_i\left(P_i\right) = a_i + b_i P_i + c_i P^2_i $ .......... $(1)$

where $a_i$, $b_i$, and $c_i$ are the function coefficients and tabulated in Table 1.

$\bullet$ The network losses are modeled, by using Kron's loss formula, as follows:

$P_L = \sum_{i=1}^{n} \sum_{j=1}^{n} P_i B_{ij} P_j + \sum_{i=1}^{n} B_{0i} P_i + B_{00}$ .......... $(2)$

where $B_{ij}$, $B_{0i}$, and $B_{00}$ are called loss coefficients (or just B-coefficients) and listed below:

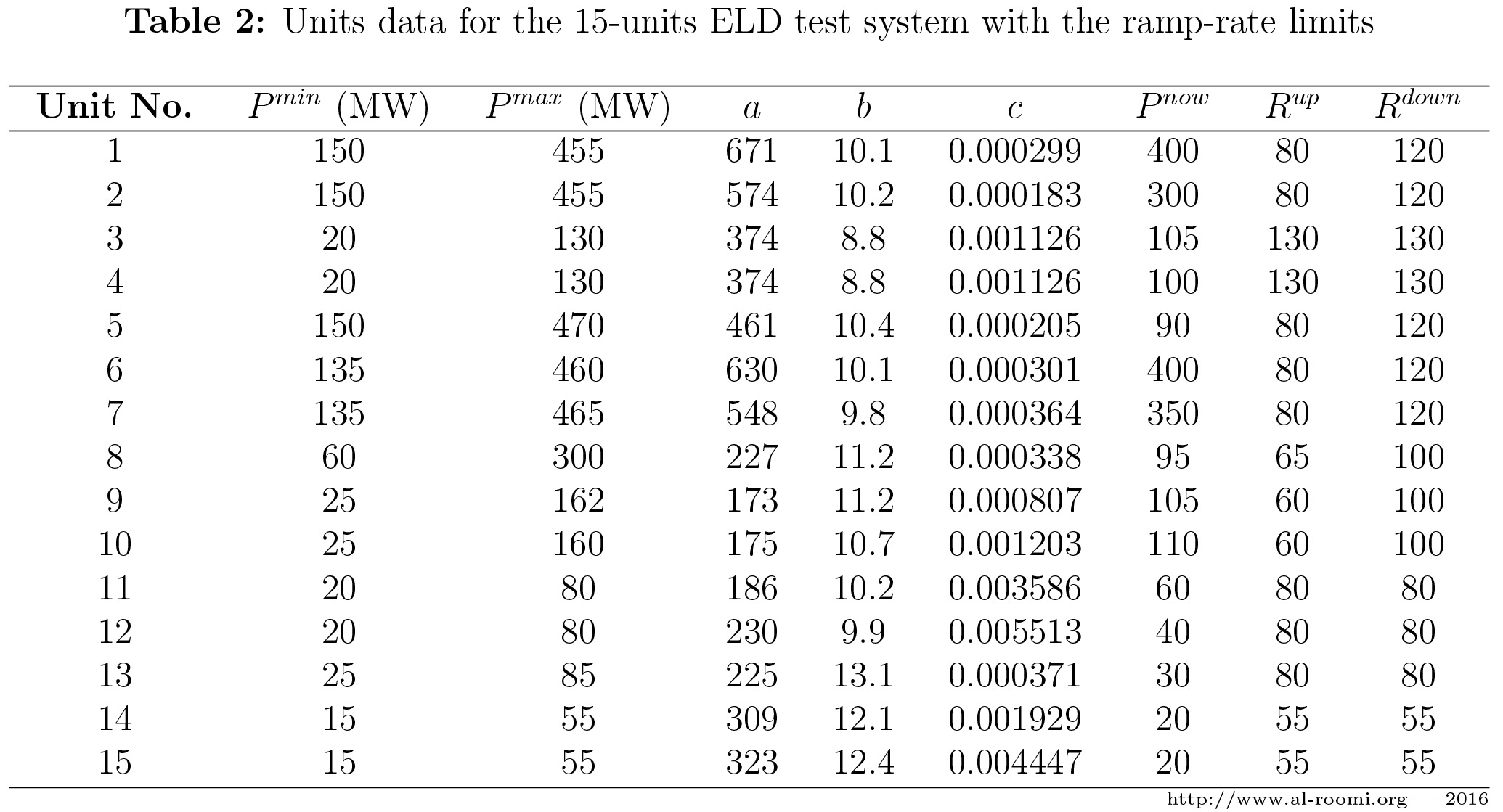
$\bullet$ If the ramp-rate limits are modeled as constraints in the design function, then the feasible search space of each unit is determined through the following equation:

$\text{max}\left(P_i^{min},P_i^{now}-R_i^{down}\right) \leqslant P_i^{new} \leqslant \text{min}\left(P_i^{max},P_i^{now}+R_i^{up}\right)$ .......... $(3)$

where $P_i^{now}$ and $P_i^{new}$ are respectively the existing and new power output of the $i$th generator. $R_i^{down}$ and $R_i^{up}$ are respectively the downward and upward ramp-rate limits, which are tabulated in Table 2.

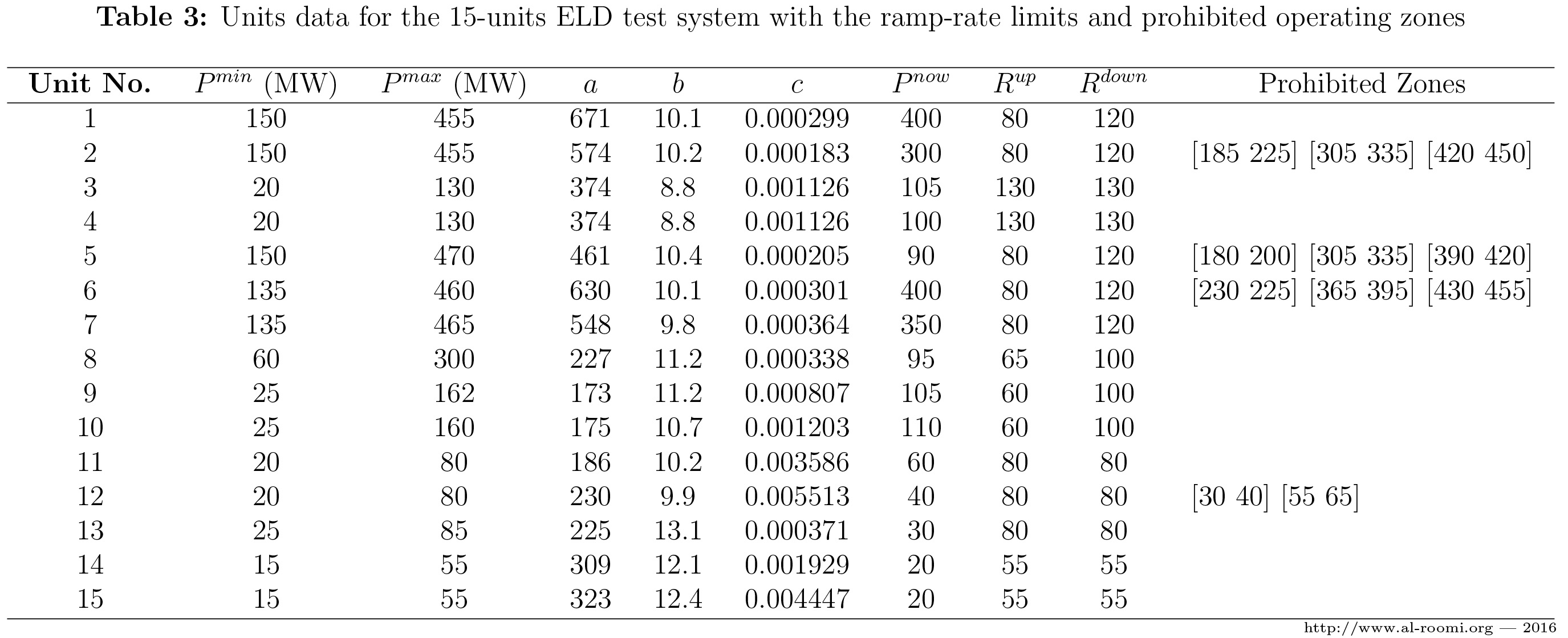
$\bullet$ Also, if the prohibited operating zone phenomenon is considered in the design function of the ELD problem, then the fuel-cost curves will have some discontinuities. This constraint can be modeled as follows:

\begin{align} P_i^{min} & \leqslant P_i \leqslant P_{i,j}^L \\ P_{i,j}^U & \leqslant P_i \leqslant P_{i,j+1}^L \text{ .......... $(4)$}\\ P_{i,\varkappa_i}^U & \leqslant P_i \leqslant P_i^{max}\end{align}

where $P_{i,j}^L$ and $P_{i,j}^U$ are respectively the lower and upper bounds of the $j$th prohibited operating zone on the fuel-cost curve of the $i$th unit. $\varkappa_i$ means the total number of the prohibited operating zones exist within the $i$th unit. Based on that, Table 2 is updated to Table 3.

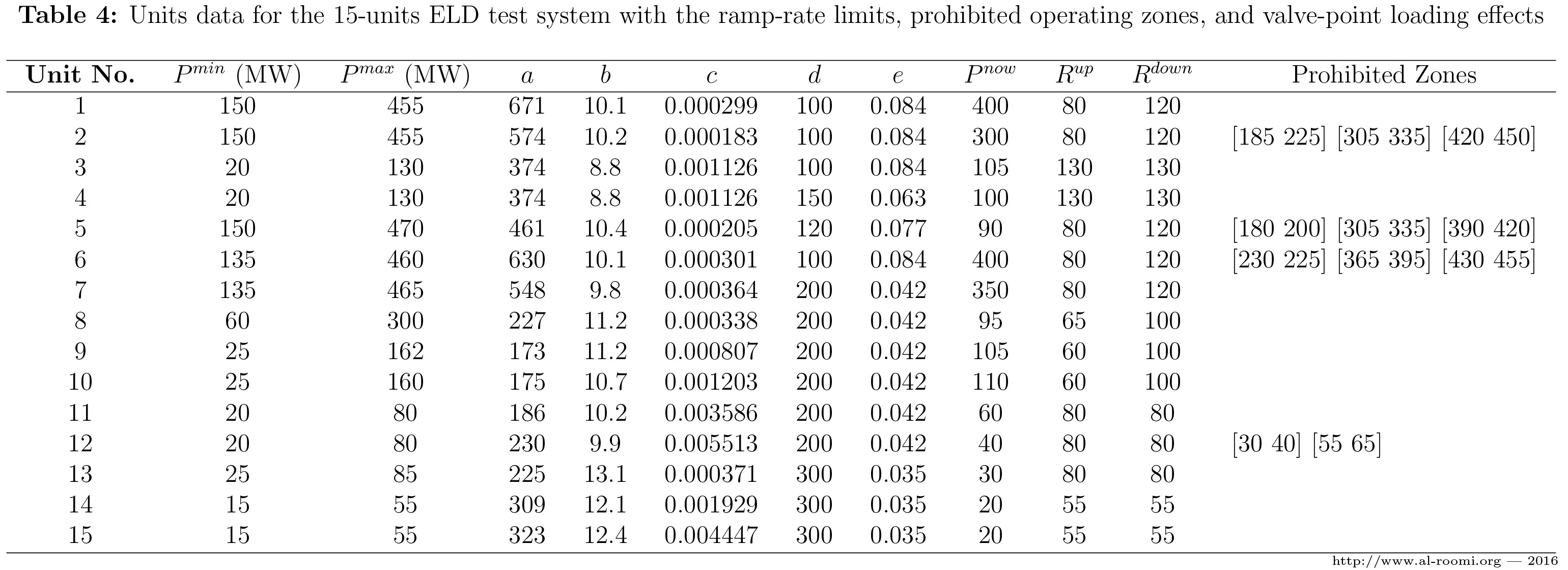
$\bullet$ In [6] and [11], the valve-point loading effects are considered in the cost function, so (1) becomes:

$C_i\left(P_i\right) = a_i + b_i P_i + c_i P^2_i + \left|d_i \times \sin\left[e_i \times \left(P_i^{min} - P_i\right) \right]\right|$ .......... $(5)$

where $d_i$ and $e_i$ are the coefficients of the valve-point loading effects. Thus, Table 3 is expanded to Table 4.

$\bullet$ The valve-point loading effects can be relaxed if either $d$ or $e$ of all units are set to zero.

II. Files:

$\bullet$ System Data (Text Format) [Download]

III. Citation Policy:

If you publish material based on databases obtained from this repository, then, in your acknowledgments, please note the assistance you received by using this repository. This will help others to obtain the same data sets and replicate your experiments. We suggest the following pseudo-APA reference format for referring to this repository:

Ali R. Al-Roomi (2016). Economic Load Dispatch Test Systems Repository [https://www.al-roomi.org/economic-dispatch]. Halifax, Nova Scotia, Canada: Dalhousie University, Electrical and Computer Engineering.

Here is a BiBTeX citation as well:

@MISC{Al-Roomi2016,
author = {Ali R. Al-Roomi},
title = {{Economic Load Dispatch Test Systems Repository}},
year = {2016},
address = {Halifax, Nova Scotia, Canada},
institution = {Dalhousie University, Electrical and Computer Engineering},
url = {https://www.al-roomi.org/economic-dispatch}
}

IV. References (Some selected papers that use this test system):

[1] F. N. Lee and A. M. Breipohl, “Reserve Constrained Economic Dispatch with Prohibited Operating Zones,” IEEE Trans. Power Syst., vol. 8, no. 1, pp. 246–254, 1993.
[2] Z.-L. Gaing, “Particle Swarm Optimization to Solving the Economic Dispatch Considering the Generator Constraints,” IEEE Trans. Power Syst., vol. 18, no. 3, pp. 1187–1195, Aug. 2003.
[3] L. dos S. Coelho and V. C. Mariani, “Improved Differential Evolution Algorithms for Handling Economic Dispatch Optimization with Generator Constraints,” Energy Convers. Manag., vol. 48, no. 5, pp. 1631–1639, Jan. 2007.
[4] K. T. Chaturvedi, M. Pandit, and L. Srivastava, “Self-Organizing Hierarchical Particle Swarm Optimization for Nonconvex Economic Dispatch,” IEEE Trans. Power Syst., vol. 23, no. 3, pp. 1079–1087, Aug. 2008.
[5] C. C. Kuo, “A Novel Coding Scheme for Practical Economic Dispatch by Modified Particle Swarm Approach,” IEEE Trans. Power Syst., vol. 23, no. 4, pp. 1825–1835, Nov. 2008.
[6] G. Shabib, M. A. Gayed, and A. M. Rashwan, “Modified Particle Swarm Optimization for Economic Load Dispatch with Valve-Point Effects and Transmission Losses,” Curr. Dev. Artif. Intell., vol. 2, no. 1, pp. 39–49, 2011.
[7] M. I. Abouheaf, S. Haesaert, W. Lee, and F. L. Lewis, “Q-Learning with Eligibility Traces to Solve Non-Convex Economic Dispatch Problems,” Int. J. Electr. Robot. Electron. Commun. Eng., vol. 6, no. 7, pp. 41–48, 2012.
[8] A. Nazari and A. Hadidi, “Biogeography Based Optimization Algorithm for Economic Load Dispatch of Power System,” Am. J. Adv. Sci. Res., vol. 1, no. 3, pp. 99–105, Sep. 2012.
[9] G. Xiong, D. Shi, and X. Duan, “Multi-Strategy Ensemble Biogeography-Based Optimization for Economic Dispatch Problems,” Appl. Energy, vol. 111, pp. 801–811, Jun. 2013.
[10] K. Zare and T. G. Bolandi, “Modified Iteration Particle Swarm Optimization Procedure for Economic Dispatch Solving with Non-Smooth and Non-Convex Fuel Cost Function,” in 3rd IET International Conference on Clean Energy and Technology (CEAT) 2014, 2014, pp. 1–6.
[11] Hardiansyah, “Modified Differential Evolution Algorithm for Economic Load Dispatch Problem with Valve-Point Effects,” Int. J. Adv. Res. Electr. Electron. Instrum. Eng., vol. 3, no. 11, pp. 13400–13409, Nov. 2014.