Price's Transistor Modelling Problem

I. Mathematical Expression:

$$f(X)=\gamma^2(X)+\sum_{k=1}^{4}\left(\alpha^2_k(X)+\beta^2_k(X)\right)$$

where:

\(\bullet\) \(\alpha_k(X)=\left(1-x_1x_2\right)x_3\left[e^{\displaystyle x_5\left(g_{1,k}-g_{3,k} \ x_7 \times 10^{-3} -g_{5,k} \ x_8 \times 10^{-3}\right)}-1\right]-g_{5,k}+g_{4,k} \ x_2\)

\(\bullet\) \(\beta_k(X)=\left(1-x_1x_2\right)x_4\left[e^{\displaystyle x_6\left(g_{1,k}-g_{2,k}-g_{3,k} \ x_7 \times 10^{-3} +g_{4,k} \ x_9 \times 10^{-3}\right)}-1\right]-g_{5,k} \ x_1+g_{4,k}\)

\(\bullet\) \(\gamma(X)=x_1x_3-x_2x_4\)

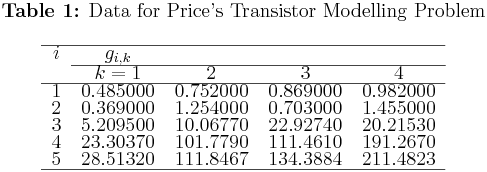
\(\bullet\) The values of \(g\) are tabulated in Table 1

\(\bullet\) \(-10\leq x_i\leq 10\) , \(i=1,2,\cdots,9\)

\(\bullet\) \(f_{min}(X^*)=0\)

\(\bullet\) \(x^*_i=(0.9,0.45,1,2,8,8,5,1,2)\)

II. Citation Policy:

If you publish material based on databases obtained from this repository, then, in your acknowledgments, please note the assistance you received by using this repository. This will help others to obtain the same data sets and replicate your experiments. We suggest the following pseudo-APA reference format for referring to this repository:

Ali R. Al-Roomi (2015). Unconstrained Single-Objective Benchmark Functions Repository [https://www.al-roomi.org/benchmarks/unconstrained]. Halifax, Nova Scotia, Canada: Dalhousie University, Electrical and Computer Engineering.

Here is a BiBTeX citation as well:

@MISC{Al-Roomi2015,
author = {Ali R. Al-Roomi},
title = {{Unconstrained Single-Objective Benchmark Functions Repository}},
year = {2015},
address = {Halifax, Nova Scotia, Canada},
institution = {Dalhousie University, Electrical and Computer Engineering},
url = {https://www.al-roomi.org/benchmarks/unconstrained}
}

III. References:

[1] M. M. Ali, C. Khompatraporn, and Z. B. Zabinsky, "A Numerical Evaluation of Several Stochastic Algorithms on Selected Continuous Global Optimization Test Problems," Journal of Global Optimization, vol. 31, no. 4, pp. 635-672, Apr. 2005.
[2] Ali R. Alroomi, "The Farm of Unconstrained Benchmark Functions," University of Bahrain, Electrical and Electronics Department, Bahrain, Oct. 2013. [Online]. Available: http://www.al-roomi.org/cv/publications